This is a question that came up today on Twitter, and is actually something I’ve been meaning to blog about.

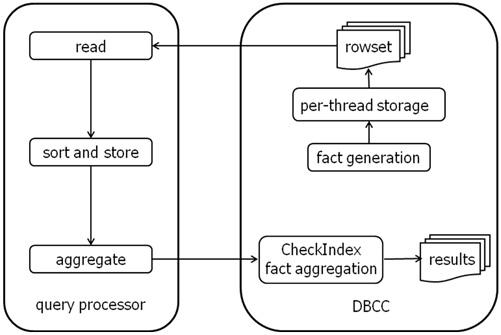
One of the biggest space hogs in tempdb can be DBCC CHECKDB. It generates all kinds of information about what it’s seeing in the database (called facts) and stores them in a giant worktable. A fact may be something like ‘we read page F’ or ‘record X on page Y points to an off-row LOB column in record A of page B’ or it could be something like an entire IAM page bitmap. It is usually the case that the amount of memory required for the worktable is more than is available to store it in memory and so the worktable spills out to tempdb.

DBCC CHECKDB needs to use this fact generation method because it doesn’t read the data file pages in any kind of logical or depth-first order – it reads them in allocation order, which is the fastest way. In fact it spawns multiple threads and each thread reads a set of pages, which is why I/O performance is sucked down while it is running – its special readahead drives the I/O subsystem as hard as it can. As each thread is generating all the facts, it hands them to the query processor which sorts them by a key DBCC CHECKDB defines (page ID, object ID, index ID etc) and inserts them into the worktable.

Once fact generation has finished, the query processor then gives the facts back to DBCC CHECKDB again so that it can match them up (e.g. page X points to page Y, so we better have seen page Y) – called the aggregation phase. If any mismatched or extra facts are found, that indicates a corruption and the relevant error is generated.

Here’s a picture of the process:

facts How does DBCC CHECKDB WITH ESTIMATEONLY work?

Now, because DBCC CHECKDB can use up so much tempdb space, we put in a way to ask it to estimate how much tempdb space will be required – it’s called WITH ESTIMATEONLY. The output looks something like:

Estimated TEMPDB space needed for CHECKALLOC (KB)
————————————————-
56
(1 row(s) affected)

Estimated TEMPDB space needed for CHECKTABLES (KB)
————————————————–
3345
(1 row(s) affected)

DBCC execution completed. If DBCC printed error messages, contact your system administrator.

This isn’t the total amount of space required to check the entire database, because DBCC CHECKDB never checks the entire database in one go (unless using the new trace flag 2562). To try to limit the amount of tempdb space required, it breaks the database down into batches. Batches are built by adding in more and more tables until one of the following limits is reached:

  • There are 512 or more indexes in the batch
  • The total estimate for facts for this batch is more than 32MB

The smallest possible batch is one table and all its indexes – so a very large table may easily blow the 32MB fact limit (or theoretically the 512 index limit).

The fact size estimation is calculated by looping through all partitions of all indexes for a table (remember a non-partitioned table or index is a special case of a single partition as far as SQL Server is concerned) and adding up:

  • Twice the sum of all pages allocated to the partition (HoBt, LOB, and SLOB)
  • Three times the number of HoBt pages in the clustered index
  • Two times the number of LOB columns in the table
  • Two times the number of tables rows, if a heap
  • Maximum row size times the number of HoBt pages

And these totals are multiplied by the sizes of the relevant facts.

The WITH ESTIMATEONLY option runs through all the batches and spits out the largest total fact estimate from all the batches. It’s supposed to be a very conservative estimate, but certain pathological cases can trip it up as it can’t account for all possible schemas.

One more piece of knowledge I can safely page-out of my head now! :-)

PS Beware also that I’ve heard of many cases of a bug in SQL Server 2008 R2 where the output is incorrectly very low. The dev team is aware of this issue and are working on it. It also seems to be broken in SQL Server 2012.

Related Posts