Multi-column statistics and exponential backoff

After writing SQLskills procs to analyze data skew and create filtered statistics, I received a couple of emails asking me to further explain the sentence “This is also true for multi-column, column statistics (where you need to use MORE than just the first column) and hypothetical indexes created with auto pilot.” (NOTE: this refers to the fact that these don’t work in the new CE.)

So, in this post, I want to further explain multi-column statistics and how both the legacy and new CE would calculate selectivity using the Credit sample database. If you don’t have a copy of this, you can download a SQL Server 2008 backup from here. To reproduce everything shown in this example, you must restore this to SQL Server 2014. FYI – at the time of this blog post, I’m running SQL Server 2014 CU3 (version = 12.0.2402.0).

What CE Model are you running?

Review the default cardinality estimation model used across all of your databases:

SELECT  [name] AS 'Database Name'
    , CASE
        WHEN [compatibility_level] = 120 THEN 'New SQL Server 2014 CE Model'
        ELSE 'Legacy CE Model'
      END AS 'Cardinality Estimation Model'
FROM    [sys].[databases];
GO

What does the Legacy CE Model use if there are multi-column statistics?

Check out the indexes and statistics on the charge table:

EXEC [sp_helpstats] '[dbo].[charge]', 'all';
GO

You should see that there are ONLY statistics on existing indexes:

statistics_name          statistics_keys
------------------------ ------------------
charge_category_link     category_no
charge_provider_link     provider_no
charge_statement_link    statement_no
ChargePK                 charge_no

We’re going to run some queries against the charge table and we’re going to query against the category_no and the provider_no columns… while indexes for category_no and provider_no might be helpful, I want to drop those and just see how the estimates work with multi-column, column statistics:

DROP INDEX [charge].[charge_provider_link];
DROP INDEX [charge].[charge_category_link];
GO

Without those indexes, SQL Server does not have any column-level statistics for the category_no or provider_no columns. To help the queries we’re going to run, we’ll create a multi-column, column statistic:

CREATE STATISTICS [TestStat]
ON [dbo].[charge] ([provider_no], [category_no]);
GO

Now, we’ll see what happens when we run a query using the legacy CE model vs. the new CE model. Be sure to turn on “Show Actual Execution Plan” in the Query drop-down menu.

SELECT [ch].*
FROM [dbo].[charge] AS [ch]
WHERE [ch].[provider_no] = 434
    AND [ch].[category_no] = 10
OPTION (QUERYTRACEON 9481, QUERYTRACEON 3604, QUERYTRACEON 9204, RECOMPILE);
GO -- TF 9481 = CardinalityEstimationModelVersion 70

Looking at the showplan: 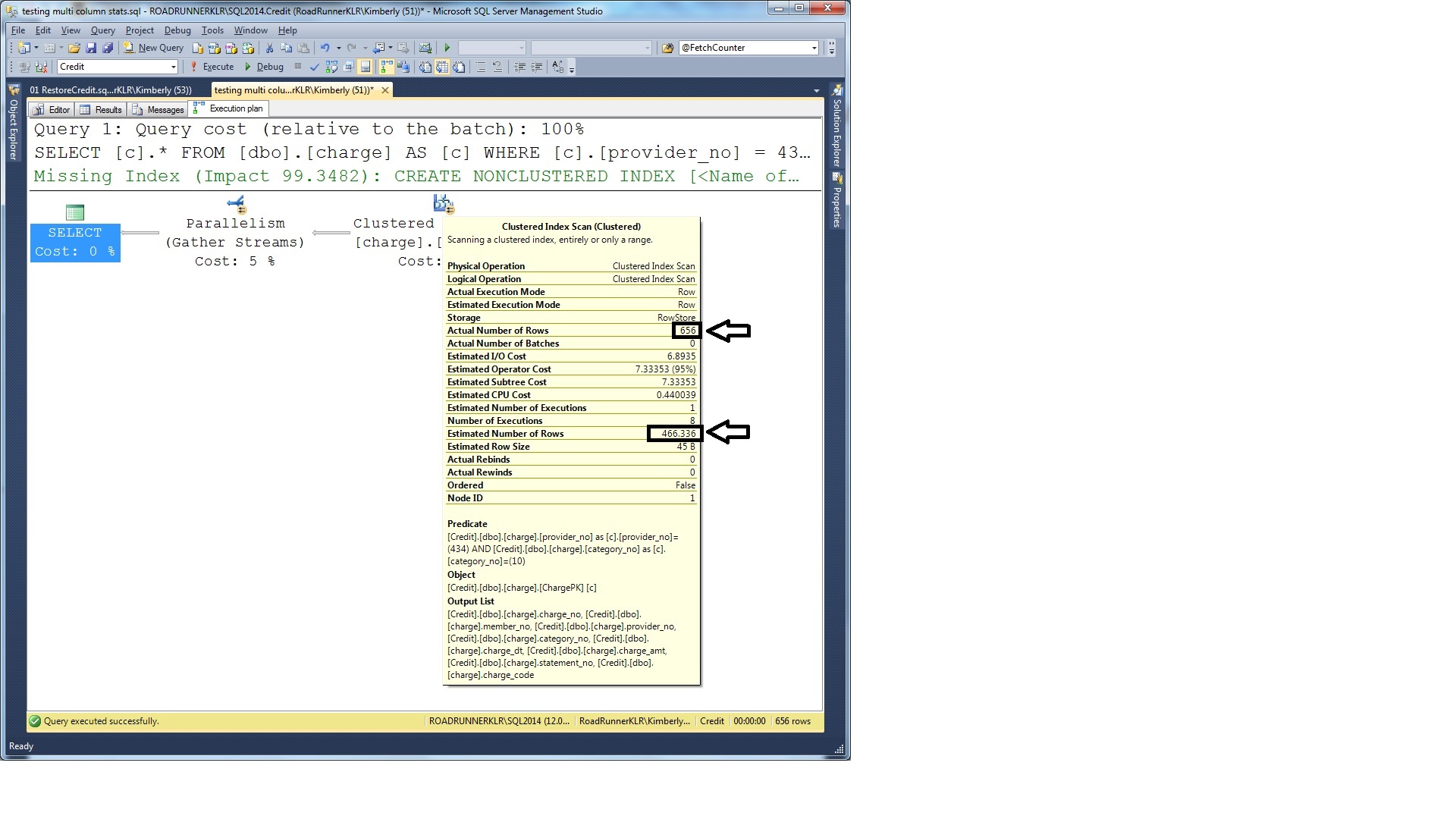You can see the estimate and the actual are fairly close (but, by no means perfect). To understand where this comes from – you need to understand the density vector component of a statistic:

DBCC SHOW_STATISTICS ('[dbo].[charge]', 'TestStat')
WITH DENSITY_VECTOR;
GO

The “All density” columns can be used to calculate the average number of rows that are returned when that column (or, combination of columns – as you add the second, third, etc. columns – shown as rows [when present] in the density vector). And, the column “Columns” shows the combination. For another example, if we had created a statistic on columns such as Lastname, Firstname, and Middleinitial then the all density could help us understand the average number of rows returned when supplying just a lastname; or, when supplying both a lastname AND a firstname; or, finally, when supplying a lastname, firstname, and middleinitial. What the density vector does not provide is a way of knowing the selectivity of any of the secondary columns on their own; it knows ONLY of the left-based combinations. This is one of the reasons why column-level statistics are helpful; they can provide the densities of the secondary columns on their own.

For this query, we’re going to use the “All density” of the combination of  provider_no and category_no (from the 2nd row of output). The “All density” value is 0.0002914602. If we multiple that by the number of rows in the table (at the time the statistics were created) then we can get the average number of rows returned. To see the number of rows in the table, we need to review the statistics_header component as well as the density_vector. This is easiest by re-running our DBCC command without the WITH clause.

DBCC SHOW_STATISTICS ('[dbo].[charge]', 'TestStat');
GO

The result is to multiply the “All density” of 0.0002914602 times 1600000 rows for an average of: 466.3363200000 (this is where the estimate of 466.336 is calculated).

What about the New CE Model in SQL Server 2014?

First, we’ll re-run the query but force the new CE model using trace flag 2312:

SELECT [ch].*
FROM [dbo].[charge] AS [ch]
WHERE [ch].[provider_no] = 434
AND [ch].[category_no] = 10
OPTION (QUERYTRACEON 2312, QUERYTRACEON 3604, QUERYTRACEON 9204, RECOMPILE);
GO -- TF 2312 = CardinalityEstimationModelVersion 120

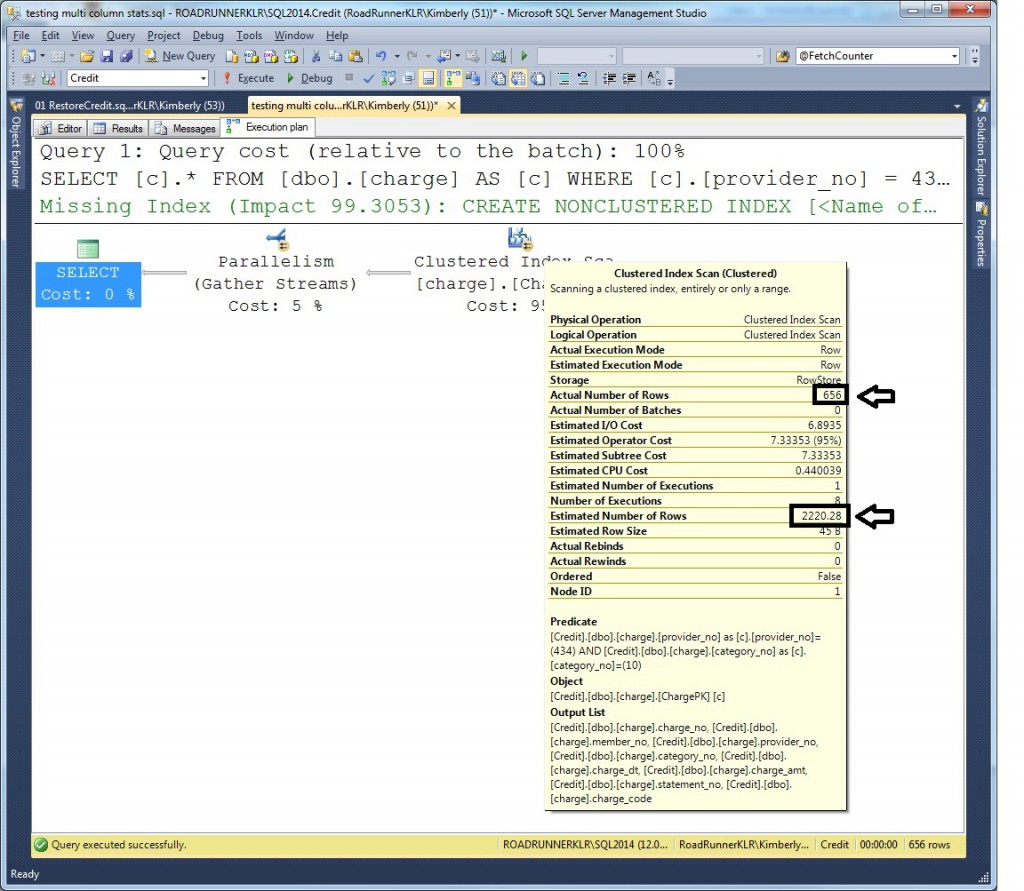
And, now we see the same plan – but, this time, the estimate is further off from the actual. And, another question might be – where did that number come from?

In SQL Server 2014, regardless of multi-column statistics, the estimate for multiple conjunctive (AND) predicates is calculated using exponential back-off. The idea is that they take the highest selectivity first and then multiply that by the subsequent square roots of the next three less selective predicates. Specifically:

most-selective-predicate * sqrt(next most selective predicate) * sqrt(sqrt(next most selective predicate)) * sqrt(sqrt(sqrt(next most selective predicate)))

In this case, they first need to calculate the selectivity of the two predicates supplied:

To calculate the selectivity for [provider_no] = 434, use the histogram from the TestStat multi-column statistic (but, they don’t use the density vector of the combination). The histogram actually has a step for 434 and it shows 6625.247 rows in the EQ_ROWS column. The selectivity of this can be calculated as 6625.247 / 1600000 OR 0.00414077937.

To calculate the selectivity for [category_no] = 10, use the histogram from the auto-created statistics on category_no (and, yes, this would have been created for this query if SQL Server hadn’t already created it for the other statement’s execution [which doesn’t entirely make sense because they didn’t use it. But, that’s another discussion for another day. And, if I’m being honest, as long as these get maintained properly, I’m ALL FOR AUTO CREATE STATS and I’d stand from the rooftops and scream it if it wouldn’t get me arrested… OK, sorry. I digress].

Once again, we’re doing well with our histograms as there’s an actual step for 10 and it shows 179692.4 rows in the EQ_ROWS column. The selectivity of this can be calculated as 179692.4 / 1600000 OR 0.112307750.

Now – to calculate our estimate… use the MOST selective predicate (0.00414077937) * the SQRT of the next most selective predicate (0.112307750) * the number of rows:

SELECT 0.00414077937 * sqrt(0.112307750) * 1600000;
GO

For:

New CE Model Estimate
----------------------
2220.27585898223

NOTE: How this is calculated may change in a later SP or CU so I can only vouch for 2014 RTM through CU3.

Sure enough, this matches our showplan output.

What would the Legacy CE Model have done without multi-column statistics?

If we had not had our multi-column statistics then the Legacy CE Model would have just expected even distribution of providers across categories. To do this they’d simply multiply the selectivities (NOT backing off at all):

SELECT 0.00414077937 * 0.112307750 * 1600000 AS [Legacy CE Model Estimate];
GO

For:

Legacy CE Model Estimate
---------------------------------------
744.06658286578800000000

Tip: Drop the ‘TestStat’ statistic and run the query again using TF 9481 to see this.

So, which CE is best?

This is where the good news and bad news comes in. There’s NO model that can deal with every type of data distribution possible. When data is evenly distributed across the different columns then the old model can produce a more accurate result:

Legacy CE Model estimate: 744.07

Multi-column statistics (just the AVERAGE of provider and category TOGETHER and across ALL values): 466.34

New CE Model estimate: 2220.28

ACTUAL: 656

The point – I could create another example where the New CE Model is the best. Here the Legacy CE is the best but the legacy CE doesn’t even use it because they rely on multi-column statistics (and therefore averages across all categories and providers). So, the irony is that they get further away with the generalized multi-column statistic. But, I could also come up with yet another example where the New CE Model produces the best result (and another where the multi-column statistic is best). In the end, it completely depends on THE DISTRIBUTION OF THE DATA.

But, the really good news is that you have a lot of troubleshooting and control options here. My recommendation (you can read more about it in the post I linked to at the start of this post) is that you STAY using the Legacy CE Model and where estimates are OFF (or, where you’re troubleshooting a suspected cardinality estimation problem), TRY the new CE using the QUERYTRACEON option. You can even try TF 4137 (this has been available since SQL Server 2008*) if you know that one value is a direct subset of the other (TF 4137 uses the MINIMUM selectivity of the predicates and does NOT perform a calculation).

Above all – have fun!
kt

* Thanks to Pedro for reminding me to mention that TF 4137 has been around since SQL Server 2008. So, if you have predicates that are subsets of the others (WHERE city = ‘Chicago’ AND state = ‘IL’ AND country = ‘USA’) then you would NOT want EITHER model to estimate (even exponential back-off is going to be wrong here even though it will be higher than the old model). Here, Chicago is a subset of IL and IL a subset of USA. Using the MINIMUM selectivity of these predicates (which would be the selectivity of Chicago) would be best. However, if you had any other predicates in there – then, all bets are off. See – this is SUPER HARD! ;-) ;-)